Skip to main content
search

Bir Çemberin Alanı, Çevresi ve Orijine Uzaklığının Hesaplanması

March 19, 2013 March 28th, 2013

İçerik

SORU 1

cember01 isimli bir fonksiyon yazın. Fonksiyonun girişleri sırasıyla aşağıdaki gibi olmalıdır:

  • Çemberin merkezinin x koordinatı (xc)
  • Çemberin merkezinin y koordinatı (yc)
  • Çemberin yarıçapı (r)
  • Çizim yapılıp yapılmayacağını gösteren bir parametre (cizdir)

Fonksiyonun çıktıları da sırasıyla aşağıdaki gibi olmalıdır:

  • Çemberin alanı (alan)
  • Çemberin çevresi (cevre)
  • Çemberin merkezinin orijine uzaklığı (uzaklik)

Ayrıca, eğer cizdir parametresi true olarak verilirse bir şekil üzerine:

  • Mavi düz cizgi ile çember çizdirilmeli,
  • Çarpı (x) işarei ile çemberin merkezi işaretlenmeli,
  • Kesikli kırmızı çizgi ile çemberin içine sığacak en büyük kare çizdirilmeli
  • Kesikli kırmızı çizgi ile çemberin içine alacak en küçük kare çizdirilmelidir.

Yukarıda belirtilen tüm çizimler, AYNI şekil üzerinde olmalıdır. Eğer cizdir parametresi false olarak verilirse herhangi bir şekil açılmamalı ve çizim yapılmamalıdır.

SORU 1’deki fonksiyonun bir örnek kullanımı

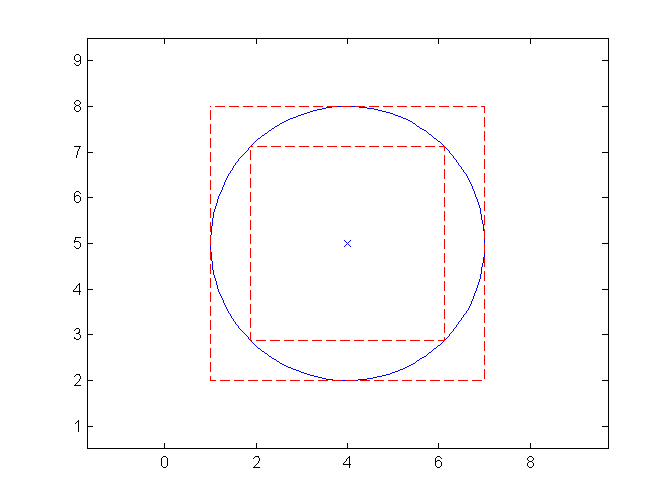
Merkezi (4,5) ve yarıçapı 3 olan çember için alan, çevre, merkezin orijine olan uzaklığını hesapla, çemberi ve iç-dış kareleri çizdir:

[alan, cevre, uzaklik] = cember01(4,5,3,true)
alan =

   28.2743

cevre =

   18.8496

uzaklik =

    6.4031

SORU 1’deki fonksiyonun başka bir örnek kullanımı

Merkezi (-1,-3) ve yarıçapı 5 olan çember için alan, çevre, merkezin orijine olan uzaklığını hesapla, şekil çizdirme:

[alan, cevre, uzaklik] = cember01(-1,-3,5,false)
alan =

   78.5398

cevre =

   31.4159

uzaklik =

    3.1623

SORU 2

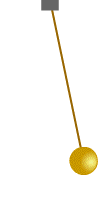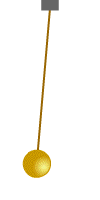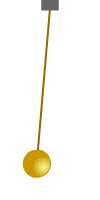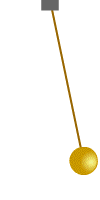
Yukarıdaki sarkaç sisteminin hareketini tanımlayan türevsel deneklemler aşağıdaki gibi yazılabilir: 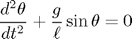$$ \frac{d^2\theta}{dt^2}+ \frac{g}{\ell} \sin \theta=0 $$

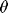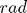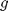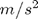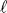Burada $\theta$ sarkacın dikey eksenle yaptığı açı ($rad$), $g$ yerçekimi ivmesi ($m/s^2$) ve $\ell$ de çubuğun uzunluğudur ($m$).

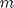Bu denklemleri çözdüren ve çizdiren bir sarkac01 fonksiyonu yazın. Fonksiyonun girişleri sırasıyla aşağıdaki gibi olmalıdır:

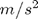  • $m/s^2$ cinsinder yerçekimi ivmesi (g)
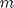  • $m$ cinsinden çubuğun uzunluğu (l)
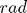  • $rad$ cinsinden başlangıç açısı (theta0)
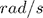  • $rad/s$ cinsinder başlangıç açısal hızı (dtheta0)
  • Saniye cinsinden simülasyon zamanı (tson)

Fonksiyonun çıktıları da sırasıyla aşağıdaki gibi olmalıdır:

  • Çözümün hesaplandığı zaman anlarından oluşan vektör (t)
  • t anlarındaki açı değerlerinden oluşan vektör (theta). Açı değeri her zaman $[-\pi,\pi]$ aralığında verilmelidir. ode çözücüleri bu aralığın dışında değerler verse bile (mesela sarkacın takla attığı durumlarda), fonksiyon çıkışında bunlar düzeltilmelidir.
  • t anlarındaki açısal hız değerlerinden oluşan vektör (dtheta)

Fonksiyon ayrıca aşağıdakileri de ekrana AYNI şekil üzerinde çizdirmelidir:

  • [0,tson] aralığında açının değişimi (mavi düz koyu çizgiyle)
  • [0,tson] aralığında açısal hızın değişimi (yeşil düz koyu çizgiyle)

Çizimin başlığı ve eksenlerin isimlendirmesi olmalıdır.

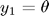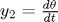İPUCU: Türevsel denklemi MATLAB’ın çözebileceği formata getirmek için öncelikle sadece birinci türevin olduğu denklemler yazmalıyız. Bunun için $y_1 = \theta$ ve $y_2 = \frac{d \theta}{d t}$ olarak iki elemanlı bir 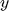$y$ vektörü düşünün ve türevini hesaplayan bir fonksiyon yapın. Ondan sonra bu fonksiyonu ve ode fonksyonlarını kullarak çözümü elde edin. Birden fazla değişken içeren adi türevsel denklemlerin (ODE) çözümüyle ilgili örnekler için yardım dokümanına bakabilirsizin. (doc ode45 yazarak bu dokümana ulaşabilirsiniz)

SORU 2’deki fonksiyonun bir örnek kullanımı

Yerçekimi ivmesi 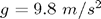$g = 9.8 \ m/s^2$, çubuk uzunluğu 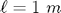$\ell = 1 \ m$ için başlangıçta 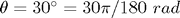$\theta = 30^\circ = 30\pi/180 \ rad$ açıyla ve hareketsiz olarak (yani 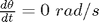$\frac{d \theta}{d t}=0 \ rad/s$) olarak duran sarkacın $6$ saniyelik hareketi:

[t, theta, dtheta] = sarkac01(9.8,1,30*pi/180,0,6)
t =

         0
    0.0000
    0.0000
    0.0000
    0.0000
    0.0001
    0.0001
    0.0002
    0.0002
    0.0005
    0.0008
    0.0010
    0.0013
    0.0026
    0.0038
    0.0051
    0.0064
    0.0128
    0.0192
    0.0256
    0.0320
    0.0641
    0.0961
    0.1281
    0.1602
    0.2207
    0.2811
    0.3416
    0.4021
    0.4703
    0.5385
    0.6067
    0.6749
    0.7356
    0.7962
    0.8569
    0.9176
    0.9862
    1.0548
    1.1235
    1.1921
    1.2547
    1.3173
    1.3799
    1.4425
    1.5108
    1.5792
    1.6475
    1.7158
    1.7773
    1.8387
    1.9001
    1.9616
    2.0309
    2.1002
    2.1696
    2.2389
    2.3026
    2.3662
    2.4299
    2.4935
    2.5621
    2.6306
    2.6991
    2.7677
    2.8302
    2.8927
    2.9552
    3.0177
    3.0880
    3.1583
    3.2287
    3.2990
    3.3640
    3.4289
    3.4939
    3.5589
    3.6276
    3.6963
    3.7650
    3.8337
    3.8976
    3.9615
    4.0253
    4.0892
    4.1608
    4.2324
    4.3040
    4.3756
    4.4420
    4.5084
    4.5749
    4.6413
    4.7100
    4.7787
    4.8475
    4.9162
    4.9818
    5.0475
    5.1131
    5.1787
    5.2455
    5.3122
    5.3789
    5.4457
    5.5129
    5.5801
    5.6473
    5.7145
    5.7777
    5.8408
    5.9040
    5.9671
    5.9754
    5.9836
    5.9918
    6.0000

theta =

    0.5236
    0.5236
    0.5236
    0.5236
    0.5236
    0.5236
    0.5236
    0.5236
    0.5236
    0.5236
    0.5236
    0.5236
    0.5236
    0.5236
    0.5236
    0.5235
    0.5235
    0.5232
    0.5227
    0.5220
    0.5211
    0.5136
    0.5011
    0.4838
    0.4619
    0.4084
    0.3408
    0.2612
    0.1724
    0.0650
   -0.0453
   -0.1536
   -0.2549
   -0.3355
   -0.4043
   -0.4589
   -0.4975
   -0.5206
   -0.5208
   -0.4980
   -0.4531
   -0.3947
   -0.3216
   -0.2363
   -0.1421
   -0.0332
    0.0773
    0.1841
    0.2827
    0.3606
    0.4254
    0.4750
    0.5077
    0.5232
    0.5152
    0.4839
    0.4307
    0.3647
    0.2846
    0.1933
    0.0945
   -0.0161
   -0.1259
   -0.2299
   -0.3234
   -0.3962
   -0.4541
   -0.4953
   -0.5184
   -0.5218
   -0.5011
   -0.4571
   -0.3917
   -0.3150
   -0.2255
   -0.1267
   -0.0228
    0.0881
    0.1949
    0.2928
    0.3773
    0.4408
    0.4873
    0.5150
    0.5231
    0.5086
    0.4697
    0.4080
    0.3265
    0.2365
    0.1365
    0.0306
   -0.0767
   -0.1842
   -0.2832
   -0.3693
   -0.4388
   -0.4869
   -0.5153
   -0.5229
   -0.5094
   -0.4748
   -0.4203
   -0.3479
   -0.2608
   -0.1617
   -0.0556
    0.0530
    0.1593
    0.2529
    0.3367
    0.4076
    0.4631
    0.4691
    0.4747
    0.4801
    0.4852

dtheta =

         0
   -0.0001
   -0.0001
   -0.0002
   -0.0002
   -0.0005
   -0.0007
   -0.0010
   -0.0012
   -0.0025
   -0.0037
   -0.0050
   -0.0062
   -0.0125
   -0.0188
   -0.0251
   -0.0313
   -0.0627
   -0.0941
   -0.1254
   -0.1567
   -0.3121
   -0.4648
   -0.6133
   -0.7564
   -1.0070
   -1.2245
   -1.4005
   -1.5282
   -1.6079
   -1.6147
   -1.5478
   -1.4114
   -1.2380
   -1.0226
   -0.7731
   -0.4986
   -0.1696
    0.1663
    0.4954
    0.8044
    1.0575
    1.2732
    1.4424
    1.5580
    1.6171
    1.6025
    1.5146
    1.3588
    1.1680
    0.9369
    0.6741
    0.3891
    0.0529
   -0.2855
   -0.6120
   -0.9130
   -1.1555
   -1.3551
   -1.5030
   -1.5926
   -1.6193
   -1.5717
   -1.4522
   -1.2677
   -1.0514
   -0.7982
   -0.5173
   -0.2191
    0.1248
    0.4634
    0.7821
    1.0668
    1.2880
    1.4587
    1.5703
    1.6179
    1.5961
    1.5010
    1.3376
    1.1150
    0.8653
    0.5843
    0.2826
   -0.0289
   -0.3765
   -0.7075
   -1.0066
   -1.2593
   -1.4410
   -1.5622
   -1.6164
   -1.6012
   -1.5134

   -1.3571
   -1.1402
   -0.8740
   -0.5859
   -0.2760
    0.0441
    0.3626
    0.6728
    0.9568
    1.2025
    1.3991
    1.5379
    1.6097
    1.6103
    1.5401
    1.4131
    1.2329
    1.0070
    0.7450
    0.7088
    0.6722
    0.6352
    0.5978

SORU 2’deki fonksiyonun başka bir örnek kullanımı

Yerçekimi ivmesi 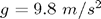$g = 9.8 \ m/s^2$, çubuk uzunluğu 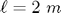$\ell = 2 \ m$ için başlangıç açıcısı 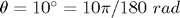$\theta = 10^\circ = 10\pi/180 \ rad$ ve başlangıç hızı 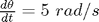$\frac{d \theta}{d t}= 5 \ rad/s$ olan sarkacın 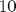$10$ saniyelik hareketi:

[t, theta, dtheta] = sarkac01(9.8,2,10*pi/180,5,10)
t =

         0
    0.0018
    0.0035
    0.0053
    0.0070
    0.0158
    0.0246
    0.0333
    0.0421
    0.0859
    0.1298
    0.1736
    0.2174
    0.3004
    0.3834
    0.4664
    0.5494
    0.6515
    0.7536
    0.8557
    0.9578
    1.0781
    1.1984
    1.3188
    1.4391
    1.5422
    1.6453
    1.7485
    1.8516
    1.9358
    2.0200
    2.1042
    2.1884
    2.2726
    2.3568
    2.4410
    2.5252
    2.6412
    2.7571
    2.8730
    2.9890
    3.0913
    3.1937
    3.2961
    3.3984
    3.4745
    3.5506
    3.6267
    3.7028
    3.7789
    3.8550
    3.9311
    4.0072
    4.1026
    4.1980
    4.2934
    4.3888
    4.5029
    4.6171
    4.7313
    4.8455
    4.9439
    5.0423
    5.1407
    5.2391
    5.3158
    5.3924
    5.4690
    5.5456
    5.6222
    5.6988
    5.7755
    5.8521
    5.9750
    6.0980
    6.2210
    6.3439
    6.4820
    6.6202
    6.7583
    6.8964
    6.9742
    7.0521
    7.1299
    7.2077
    7.2855
    7.3634
    7.4412
    7.5190
    7.6165
    7.7140
    7.8115
    7.9090
    8.0282
    8.1474
    8.2666
    8.3858
    8.4861
    8.5864
    8.6867
    8.7871
    8.8688
    8.9506
    9.0323
    9.1141
    9.1959
    9.2776
    9.3594
    9.4411
    9.5640
    9.6869
    9.8098
    9.9327
    9.9495
    9.9663
    9.9832
   10.0000

theta =

    0.1745
    0.1833
    0.1921
    0.2008
    0.2096
    0.2533
    0.2970
    0.3405
    0.3839
    0.5986
    0.8079
    1.0105
    1.2051
    1.5490
    1.8596
    2.1381
    2.3882
    2.6651
    2.9187
   -3.1226
   -2.8797
   -2.5766
   -2.2346
   -1.8354
   -1.3683
   -0.9127
   -0.4175
    0.0982
    0.6098
    1.0061
    1.3736
    1.7077
    2.0074
    2.2756
    2.5175
    2.7389
    2.9467
   -3.0601
   -2.7781
   -2.4721
   -2.1251
   -1.7731
   -1.3711
   -0.9195
   -0.4279
   -0.0473
    0.3343
    0.7069
    1.0615
    1.3911
    1.6933
    1.9675
    2.2156
    2.4954
    2.7483
    2.9839
   -3.0707
   -2.7926
   -2.4921
   -2.1520
   -1.7588
   -1.3701
   -0.9358
   -0.4642
    0.0284
    0.4121
    0.7844
    1.1367
    1.4633
    1.7612
    2.0311
    2.2754
    2.4978
    2.8210
    3.1210
   -2.8638
   -2.5448
   -2.1377
   -1.6515
   -1.0728
   -0.4130
   -0.0199
    0.3735
    0.7565
    1.1195
    1.4557
    1.7628
    2.0411
    2.2929
    2.5777
    2.8378
    3.0836
   -2.9566
   -2.6477
   -2.3049
   -1.9089
   -1.4477
   -1.0062
   -0.5245
   -0.0188
    0.4885
    0.8856
    1.2578
    1.5994
    1.9084
    2.1864
    2.4379
    2.6682
    2.8834
   -3.0904
   -2.7766
   -2.4352
   -2.0454
   -1.9872
   -1.9277
   -1.8670
   -1.8049

dtheta =

    5.0000
    4.9985
    4.9969
    4.9952
    4.9934
    4.9836
    4.9719
    4.9584
    4.9432
    4.8420
    4.7033
    4.5340
    4.3420
    3.9449
    3.5437
    3.1749
    2.8631
    2.5765
    2.4060
    2.3557
    2.4259
    2.6568
    3.0528
    3.5863
    4.1761
    4.6365
    4.9448
    5.0219
    4.8488
    4.5518
    4.1709
    3.7585
    3.3621
    3.0168
    2.7380
    2.5360
    2.4152
    2.3822
    2.5088
    2.7923
    3.2152
    3.6781
    4.1744
    4.6290
    4.9445
    5.0322
    4.9799
    4.7946
    4.5056
    4.1560
    3.7847
    3.4254
    3.1028
    2.7743
    2.5432
    2.4165
    2.3967
    2.5105
    2.7790
    3.1910
    3.7079
    4.1894
    4.6248
    4.9313
    5.0380
    4.9561
    4.7463
    4.4389
    4.0762
    3.7027
    3.3482
    3.0357
    2.7795
    2.5023
    2.4022
    2.4834
    2.7393
    3.2067
    3.8366
    4.5145
    4.9971
    5.0790
    5.0131
    4.8091
    4.5008
    4.1362
    3.7566
    3.3971
    3.0825
    2.7748
    2.5749
    2.4894
    2.5199
    2.7090
    3.0703
    3.5789
    4.1600
    4.6235
    4.9599
    5.0881
    4.9759
    4.7228
    4.3731
    3.9767
    3.5819
    3.2278
    2.9335
    2.7117
    2.5692
    2.5058
    2.6330
    2.9469
    3.4190
    3.4934
    3.5698
    3.6480
    3.7276

Şekilden sarkacın takla attığı anlaşılabilir. Açı değerinin her zaman $[-\pi,\pi]$ arasında verildiğine dikkat ediniz. (Şekildeki zıplamalar da bu yüzden olmaktadır; aslında $-\pi=\pi$ olduğundan sarkacın hareketinde bir süreksizlik yoktur)

ÇÖZÜM

Soruların Çözümleri

Tags:

M.Eren Çelik

Author M.Eren Çelik

More posts by M.Eren Çelik
Close Menu